1. 수의 시각화
왜 수에 대해 알아야 하는가?
게임 세계는 벡터로 구성된 시스템. 이 시스템 위에서 콘텐츠가 만들어짐.
벡터는 수를 사용해 만들어진 대상이므로, 벡터를 정확히 이해하기 위해서는 결국 수가 만들어내는 시스템에 대한 이해가 필요하다.
수(Numbers)의 종류
다양한 수의 개념이 존재하며, 각각은 대문자를 사용해 집합으로 구분하여 부른다.

실수 집합(The set of real numbers) R
실수 집합 R은 수 사이에 빈틈이 없는 연속된 무한의 요소로 구성된 수의 집합임

이러한 실수 집합의 개념과 원소의 개념에서의 수를 바라보는 것을 훈련할 필요가 있음.
수 직선(Number Line)
실수 집합 R의 요소를 점으로 나열하면 연속성 있는 직선으로 표현할 수 있음.

수의 표현
하나의 체계에서 대소를 비교해 나열하는 방식

벡터 시스템에서는 하나의 체계에 기반해서 보는 것이 아닌 0을 기준으로 대칭된 두 개의 체계로 보는 것이 편리할 수 있음.
원점을 기준으로 양수와 음수의 두 체계로 나누고 크기와 방향을 사용해 표현하는 방식을 사용

이러한 관점에서의 수를 본다면 수는 두 가지의 요소로 요약됨.
- 크기 = | 𝒳 | (원점으로부터의 거리)
- 방향
수에 대해서 표현할 수 있게 됐다면 그 다음은 수가 가지고 있는 연산 시스템.
2. 이항 연산(Binary Operation)
수를 '집합'의 개념으로 관리한다.
- 집합(Set)의 정의 : 원소(Element)의 묶음(Collection)
- 수 집합이 일반적인 집합과 다른 점: 연산이 존재한다.
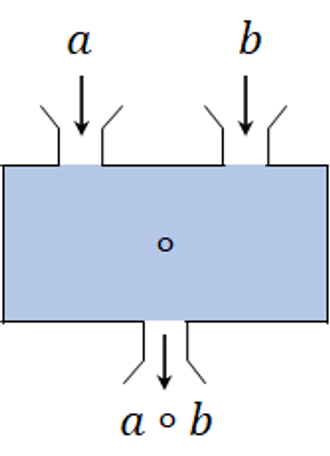
a와 b라는 두 개의 원소를 ◦ 연산을 통해 새롭게 생성한 a ◦ b (a 서클 b)
a ◦ b라는 연산의 결과물은 다시 집합에 속하게 됨.
이러한 것을 수학에서 '닫혀있다'고 표현함.
사칙 연산의 재구성
뺄셈도 덧셈, 나눗셈 또는 곱셈으로 대체해 표현이 가능

덧셈 연산(Addition)의 시각화 (벡터의 관점)
덧셈 연산은 점을 평행 이동시키는 연산

곱셈 연산(Multiplication)의 시각화 (벡터의 관점)
곱셈 연산은 원점을 중심으로 점의 크기와 방향을 조절하는 연산

가지고 있는 대상의 크기를 원점으로부터 늘리는(배율을 조정하는) 것에 방향이라는 개념이 더해짐.
1 ∙ 4의 경우:
1이 가지고 있는 크기를 4배 증가(스케일 증가)시키는데, 방향 개념이 들어감.
1이 가지고 있는 것과 같은 방향으로 4배 증가시킨 것.
2 ∙ -1의 경우:
2가 가지고 있는 크기를 1배(스케일의 변화 없이 유지)하지만 -되어 반대 방향으로 뒤집어짐(180도 회전).
곱셈에는 회전이라는 개념이 포함되어 있다.
양수의 곱셈은 0° 회전, 회전의 방향은 유지
음수의 곱셈은 180° 회전. 반대 방향으로 뒤집어짐.
3. 이항 연산의 성질
실수 집합이라고 하는 것은 구조적인 측면에서 봤을 때
수 집합과 수 집합의 연산 체계를 포괄하는 개념

이항 연산의 성질
- 교환 법칙(Commutativity) : a ∙ b = b ∙ a
연산의 순서를 반대로 뒤집어도 동일한 결과 - 결합 법칙(Associativity) : (a ∙ b) ∙ c = a ∙ (b ∙ c)
연산을 진행할 때 세 가지 원소 중 어떤 것을 먼저 계산하든 동일한 결과 - 분배 법칙(Distributivity) : 좌분배법칙 a ∙ (b + c) = a ∙ b + a ∙ c | 우분배법칙 (b + c) ∙ a = b ∙ a + c ∙ a
좌분배법칙과 우분배법칙을 모두 만족해야 분배법칙이라는 성질을 가진다고 이야기함.
항등원(Identity)
어떤 임의의 요소 a에 대해서, 연산의 결과가 동일하게(a) 나오게 만드는 원소(b)를 항등원이라 함.
° 연산에 대한 항등원은 b다.

덧셈의 항등원 : 0 ( a + 0 = a )
곱셈의 항등원 : 1 ( a ∙ 1 = a )
역원(Inverse)
연산의 결과가 항등원이 되도록 만들어주는 원소를 역원이라 함.
a의 ° 연산에 대한 항동원을 b라 할 때, ° 연산에 대한 a의 역원은 c다.

덧셈의 역원 : -a (a + -a = 0), 덧셈의 역원 → 반수(Opposite Number). 어떤 수에 반대 부호를 붙인 것
곱셈의 역원 : ⅟a (a ∙ ⅟a = 1, a ≠ 0), 곱셈의 역원 → 역수(Reciprocal). 어떤 요소를 분모로 취해 만들어지는 수
뺄셈은 덧셈의 역원을 더하는 연산 : a - b = a + (- b)
나눗셈은 곱셈의 역원을 곱하는 연산 : a ÷ b = a ∙ ⅟b
뺄셈은 교환 법칙이 성립하지는 않지만, 덧셈은 교환 법칙이 성립함. (곱셈도 마찬가지)
a - b ≠ b - a
a + (- b) = (- b) + a
∴ 사칙 연산에서 뺄셈과 나눗셈을 제하고 덧셈과 곱셈으로 연산의 구조를 분석.
4. 체(Field)의 공리(Axiom)
공리 : 이론 체계에서 증명이 필요없는 가장 기초적인 명제
공리를 사용해 다양한 수의 구조를 정의
군(Group)의 공리
첫 번째 연산에 대해 다음의 공리를 만족하는 수의 체계
- 덧셈 연산에 대해 닫혀있다. (Closure)
덧셈의 결과는 항상 그 수 집합에 속해야 함. - 덧셈 연산은 결합 법칙을 만족한다. (Associativity)
- 덧셈 연산은 항등원이 존재한다. (Identity element)
실수는 항등원이 0이기 때문에 바로 만족됨. - 덧셈 연산의 역원이 존재한다. (Inverse element)
반수가 있기 때문에 만족됨
실수는 군 구조를 가짐.

실수 집합의 심볼과 더하기 연산을 사용해 군의 구조를 가진다고 표현함.
아벨 군(Abelian Group)
1. 덧셈 연산은 교환 법칙을 만족한다. (Commutativity)
교환법칙을 만족하면 아벨 군 구조를 가진다고도 표현함.
환(Ring)의 공리
첫 번째와 두 번째 연산에 대해 다음의 공리를 만족하는 수의 체계
- 곱셈 연산에 대해 닫혀있다. (Closure)
- 곱셈 연산은 결합 법칙을 만족한다. (Associativity)
- 덧셈과 곱셈 연산은 분배 법칙을 만족한다. (Distributivity)
분배 법칙은 두 가지 연산을 사용하기 때문에 군에서 사용한 첫 번째 연산과
환에서 사용하는 두 번째 연산을 결합해 분배법칙을 만족하면 환의 구조를 가진다고 함.

실수 집합의 심볼과 더하기 연산과 곱셈 연산
가환환(Commutative Ring)
환의 구조에서 두 번째 연산에 대해 교환 법칙을 만족하고 곱셈 연산의 항등원이 존재하는 특수한 환.
- 곱셈 연산은 교환 법칙을 만족한다. (Commutativity)
- 곱셈 연산의 항등원이 존재한다. (Identity element)
체(Field)의 공리
곱셈의 역원이 존재하는 수의 구조
- 0을 제외한 모든 원소에 대해 곱셈 연산의 역원이 존재한다. (Inverse element)
→ 일반적으로 사용하는 실수는 체의 구조를 가진다. 앞서 정리된 모든 공리를 만족함.
덧셈과 곱셈 연산에 대해 교환, 결합, 분배 법칙을 만족하고 항등원과 역원이 존재하는 수의 구조
→ 사칙 연산에 닫혀있고 자유롭게 연산 순서를 적용할 수 있다.
→ 체의 구조를 만족하는 수 집합으로는 유리수(Q), 실수(R), 복소수(C)가 있음.
실질적으로 수를 다룰 때 대부분 실수의 체계에서 다루지만, 이론적인 체계에서는 체의 구조를 가진
수 집합을 사용한다고 표현하는 것이 명확하고 확장 가능성이 높아짐.
체 집합은 F로 표현하고 체 집합의 원소를 스칼라(Scalar)라고 함.

실수 집합(R)의 개념에서 원소는 실수, 체 집합(F)(구조적 개념)에서 원소는 스칼라.
수와 연산의 추상화
a + b
- 실수 a와 실수 b를 더한다 : 사칙 연산을 자유롭게 사용할 수 있으나 실수라는 하나의 수 체계만 사용
- 스칼라 a와 스칼라 b를 더한다 : 체의 성질을 만족하는 모든 수 집합(유리수, 실수, 복소수)에 대해
포괄적으로 사용 가능.
→ 범용적인 수와 연산 시스템을 규정하는 체의 기반 위에서 새로운 시스템(벡터)으로 확장할 기반이 만들어짐
게임 엔진을 지탱하는 게임 수학 강의 | 이득우 - 인프런
이득우 | 게임을 구성하는 가상 세계가 수학으로 어떻게 만들어지는지 기반에서부터 하나씩 다루는 강의입니다. 기반 수학을 통해 게임 엔진의 구성 원리를 이해하고, 3차원 공간을 구성하는 실
www.inflearn.com
'게임 개발 > 게임 수학' 카테고리의 다른 글
| 게임 수학 - 삼각 함수 (1) | 2025.02.26 |
|---|---|
| 게임 수학 - 선형 독립 (0) | 2025.02.25 |
| 게임 수학 - 벡터 (0) | 2025.02.11 |
| 게임 수학 - 함수 (0) | 2025.02.04 |
| 기초 수학 - 로그 (0) | 2024.07.23 |