1. 함수(Function)의 기초
함수를 왜 배워야 하는가?
게임의 공간을 구성하고 화면에 보여지는 전 과정은 대부분 공간과 공간의 변환으로 구성됨.
이러한 변환은 근본적으로 집합과 집합의 대응 관계에 기반하고 있으며, 이러한 메카니즘을 설명하는 이론이 함수.
함수에 대한 개념을 제대로 정립하는 것이 게임 공간과 공간의 변환을 올바르게 이해할 수 있는 기본 지식이 됨.
함수의 정의
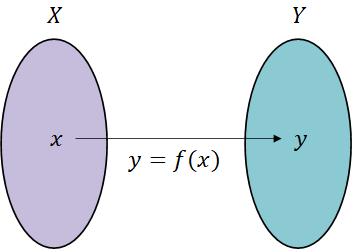
첫 번째 집합 X의 요소인 x가 두 번째 집합 요소인 y에 대응될 때, y = f(x) 라고 표기
- 함수의 성립 조건 : 첫 번째 집합의 모든 요소가 사용되어야 한다.
함수가 아닌 대응 관계
- 첫 번째 집합의 어떤 원소에 대한 대응 관계가 빠져 있을 때
첫 번째 집합의 한 원소가 두 번째 집합의 두 가지 이상의 원소에 대응할 때

함수에 관련된 주요 용어
- 정의역(Domain)
첫 번째 집합. - 공역(Codomain)
대응되는 두 번째 집합. - 치역(Range)
두 번째 집합에서 대응되는 요소들만 모아
별도로 집합을 구성한 것.

정의역의 모든 원소는 대응되어야 하는 반면,
두 번째 대응되는 집합의 모든 원소가 대응될 필요는 없음
프로그래밍 관점에서 함수를 바라보기
- 입력(Input)
대응에 사용되는 정의역의 요소 - 출력(Output)
대응되는 공역의 요소

대응 관계에 따른 함수의 종류(Classes of Function)
- 전사(Surjection) : 공역과 치역이 동일(공역의 모든 요소가 대응)
X집합의 3과 4가 1:1 대응되지 않아 단사 함수에 해당되진 않음
- 단사(Injection) : 정의역과 공역의 요소가 1:1로 대응
C가 대응되지 않기 때문에(공역과 치역이 서로 다른 집합을 구성) 전사에 해당하지 않음
- 전단사(Bijection) : 전사 + 단사를 모두 만족
정의역의 모든 요소에 대해서 공역의 모든 요소가 1:1로 대응됨
- 일반(General) : 그 외.

2. 곱집합(Cartesian Product)
곱집합의 정의
곱집합이란 두 집합의 원소를 순서쌍으로 묶어 구성한 새로운 집합.
(a,b)와 같이 괄호와 콤마를 사용해 원소를 나열하는 방식을 튜플(Tuple)이라 함.
곱집합은 × 기호를 사용해 표현. (A × B, A times B)
곱집합의 예시


수 집합 R = {A, K, Q, J, 10, 9, 8, 7, 6, 5, 4, 3, 2}
모양 집합 S = {♠,♥,♣,◆}
트럼프 : R × S
이항 연산을 함수로 해석하기

흔히 실수 집합에서 진행하는 연산(a+b) 같은 경우, 정의역을 실수 집합의 곱집합으로 만듦.
R × R 로 만들고 두 개의 순서쌍을 만들어 각각의 원소를 입력에 넣은 뒤 출력을 만들어내면
완벽한 이항 연산을 만들어내는 시스템을 함수로 표현할 수 있게 됨.
이항 연산은 두 개의 입력이 들어감 → 함수로 표현하기 어려움
하지만 정의역(입력)을 곱집합으로 사용하면 두 개의 요소를 사용해 인자로 넣을 수 있음.
→ 이항 연산을 함수로 표현할 수 있게 됨.
3. 합성함수(Composition)

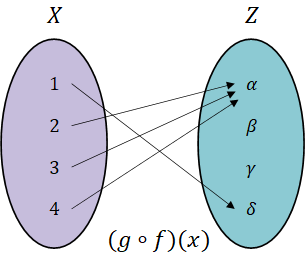
집합 X에서 집합 Z로 대응되는 관계가 반드시 성립됨.
집합 X의 4를 보면 첫 번째 함수 f(x)를 통해 집합 Y의 D에 대응되고
g(y)를 통해 집합 Z의 α에 대응되는 관계를 가짐.
결국 4 → α, 3 → α, 2 → α 로 대응되는 관계로 바로 해석할 수 있음.
중간 단계를 생략하고 바로 넘어가는 것이 합성함수의 개념.
두 개의 함수를 합성했다는 의미에서 Composition, 합성 함수라고 함.
표기할 때는 첫 번째로 사용한 함수를 오른쪽에 배치.
(g ○ f), g cirlce f 라는 형태로 표현.
대응관계
항등함수(Identity Function)

전단사 함수, 정의역의 요소와 공역(치역)의 요소가 같은, 똑같은 요소가 대응되는 관계
기호 : i
역함수(Inverse Function)

전단사 함수일 때 성립됨.
정의역에서 공역으로 대응되는 관계를, 거꾸로 공역에서 정의역으로 대응하는 관계로 나타내는 것
역함수의 조건
역함수를 만들기 위해서 그 함수는 반드시 전단사 함수여야 한다.
아래의 전사 함수는 역함수가 성립되지 않음.

공역의 a, b, c가 반대로 정의역에 대응되는 경우 c가 3과 4에 각각 대응하기 때문에
함수의 정의를 만족하지 못함.
아래의 단사 함수는 역함수가 성립되지 않음.

c에 대응되는 대응 관계가 존재하지 않기 때문에 함수의 조건을 만족하지 않음.
전단사 함수일 때만 역함수를 보장받음.

모든 요소들이 1:1로 대응되고 빠짐없이 대응되고 있기 때문에
전단사 함수일 때는 언제나 역함수가 성립됨.
함수와 그 역함수의 합성 함수


어떤 전단사 함수와 그 역함수의 합성 함수는 항등함수가 된다.
공역으로 넘어간 대응 관계가 다시 정의역으로 돌아오는 것이기 때문에
처음에 대응한 자기 자신에게 돌아오게 됨.
합성함수의 역함수



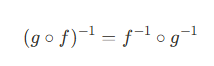
(g ○ f)의 역함수는 g의 역을 먼저 구하고 f의 역을 구한다.
왜 이러한 합성함수의 대응 관계를 알아야 하는가?
컴퓨터에서 중요하게 사용되는 행렬은 하나의 함수에 대응되고 행렬의 곱셈은 합성 함수에 대응됨.
합성 함수의 성질을 이해하면 복잡한 행렬 연산의 메커니즘을 이해할 수 있는 기반이 됨.
게임 엔진을 지탱하는 게임 수학 강의 | 이득우 - 인프런
이득우 | 게임을 구성하는 가상 세계가 수학으로 어떻게 만들어지는지 기반에서부터 하나씩 다루는 강의입니다. 기반 수학을 통해 게임 엔진의 구성 원리를 이해하고, 3차원 공간을 구성하는 실
www.inflearn.com
'게임 개발 > 게임 수학' 카테고리의 다른 글
| 게임 수학 - 삼각 함수 (1) | 2025.02.26 |
|---|---|
| 게임 수학 - 선형 독립 (0) | 2025.02.25 |
| 게임 수학 - 벡터 (0) | 2025.02.11 |
| 게임 수학 - 수의 구조 (0) | 2025.01.22 |
| 기초 수학 - 로그 (0) | 2024.07.23 |