게임 수학 - 삼각 함수

1. 삼각함수(Trigonometric function)

직각삼각형(Right-Angled Triangle)의 삼요소

 

삼각비(Trigonomertric Ratio)

직각 삼각형을 구성하는 세 요소 중 두 요소에 대한 비의 값

 

직각삼각형의 3개의 변 중 2개의 변에 대한 비를 삼각비라고 하며,

총 6가지 중 중요하게 사용되는 것이 사인, 코사인, 탄젠트 3가지. 

 

$sin=\frac{Opposite}{Hypotenuse}$

$cos=\frac{Adjacent}{Hypotenuse}$

$tan=\frac{Opposite}{Adjacent}$

 

컴퓨터 그래픽스에서는 사인함수(Sine)와 코사인함수(Cosine)를 가장 많이 사용함.

탄젠트함수(Tangent)의 경우 역함수를 사용해 벡터의 각을 구하는데 활용

 

삼각함수(Trigonometric Functinos)

삼각비를 집합의 관점에서 대응 관계로 나타낸 것

정의역: 실수 집합 $\mathbb{R}$

공역: [-1, 1]

 

빗변을 형성하는데 사용하는, 밑변과 빗변 사이의 각을 정의역으로 두고 그 값을 취했을 때

그 값은 항상 -1에서 1사이의 값을 가지게 됨. 

취하는 값에 대한 것을 정의역으로, 그 결과에 대해서 공역과 치역의 범위를 -1 ~ 1로 놓았을 때

이러한 두 집합 간 대응 관계가 생김.

 

정의역의 원소 x와 공역의 원소 y에 대한 대응 관계에 삼각비의 어떤 정의역의 값을 대입했다라는 의미로

$y = sin(x)$ 라는 함수로 표시할 수 있고, 이를 삼각 함수라 한다.

 

데카르트 평면 좌표계에서 만들어지는, 흔히 360도로 일컫는 평면의 모든 각에 대해서 일반화시킨 

어떤 대응관계가 삼각 함수.

그래서 삼각함수를 사용할 때는 직각 삼각형에 국한되어 사용하기보다는 평면을 모두 다 커버하는

단위원을 기반으로 분석하게 됨.

 

삼각함수와 단위 원

단위 원: 반지름이 1인 원

반지름이 1인 원 안에 들어가는 직각 삼각형을 생각했을 때 빗변이 단위 원의 원호의 어떤 점을 가리킨다고 가정하면

빗변의 값은 항상 원의 반지름인 1이 됨.

 

출처: https://en.wikipedia.org/wiki/Sine_and_cosine

빗변의 값이 1인 상태에서 삼각함수를 지정하게 되면 빗변 벡터를 계속해서 회전시켰을 때 위와 같은 곡선의 값이 얻어지게 되고, 이 값이 사인 함수와 코사인 함수의 그래프가 된다.

 

$cos\theta$는 $x$축의 길이, $sin\theta$는 $y$축의 길이

$tan\theta$는 빗변의 기울기라고 생각하면 쉬움.

 

 

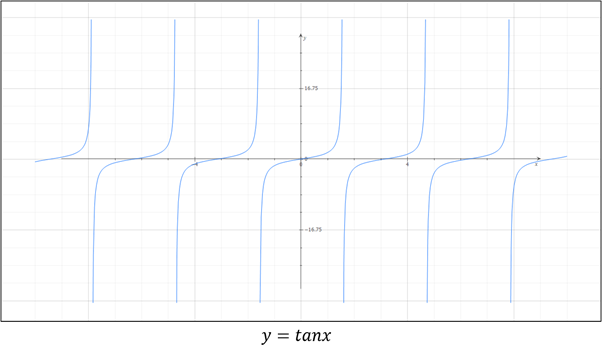
사인과 코사인 함수의 성질

1. 사인 함수와 코사인 함수는 항상 [-1, 1] 범위를 일정하게 반복되는 패턴을 가진다.

2. 사인과 코사인 함수는 $2\pi$(360^\circ) 단위로 반복된다.

3. 축을 기준으로 좌우를 포갰을 때 사인 함수는 상하 반전된 형태, 코사인 함수는 좌우 대칭인 형태를 가진다.

 

$sin(\theta) \ne sin(-\theta)$

$sin(\theta) = -sin(-\theta)$

$cos(\theta) = cos(-\theta)$

 

탄젠트 함수는 $cos90^\circ$, $cos270^\circ$에서 존재하지 않음.

$tan=\frac{sin\theta}{cos\theta}$ 인데, $\theta$가 $90^/circ, 270^\circ$일 때 ($cos90^\circ$, $cos270^\circ$) 일 때

frac{sin\theta}{0}$가 되고, 분모가 0인 경우는 존재할 수 없으므로 코사인함수 x가 0인 지점,

$cos90^\circ$, $cos270^\circ$ 에서 탄젠트 함수는 존재하지 않음.

또, $tan\theta$를 빗변의 기울기로 봤을 때(\frac{sin\theta}{cos\theta} → $\frac{y}{x}$), $cos90^\circ$, $cos270^\circ$에서

마찬가지로 분모가 0이 되어 기울기가 없기 때문에 존재하지 않는 것으로 이해할 수 있음

 

 

삼각함수의 유용한 공식

직각삼각형 = 피타고라스의 정리

$밑변^2+높이^2=빗변^2$
$cos^2\theta+sin^2\theta = 1$
$tan\theta = \frac{sin\thate}{cos\theta}$

 

원의 반지름 값이 $r$인 경우, 원호의 좌표는 ($cos\theta, sin\theta$) 벡터에 $r$배 한 결과가 나오며.

스칼라로 스케일을 업다운하는, 벡터와 스칼라의 곱셈이라고 생각할 수 있다.

삼각비를 이루기 때문의 위의 공식은 유효하다.

$r^2 cos^2\theta+r^2 sin^2\theta = r^2$

$\therefore cos^2\theta+sin^2\theta = 1$

 

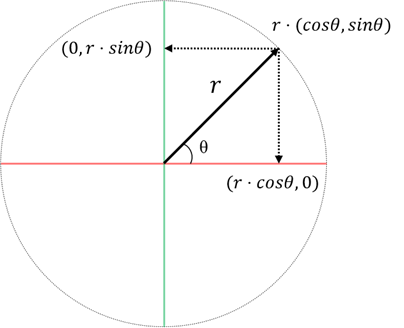
반지름 r인 원호에 위치한 좌표의 분해

$r \cdot (cos\theta, sin\theta) = (r \cdot \theta, 0) + (0, r \cdot sin\theta)$

 

실 벡터 공간 $\methbb{R}^2$의 표준 기저 벡터 = 크기가 1인 벡터 = $cos\theta, cin\theta$ = 각의 값이 $0^\circ$와 $90^\circ$에 해당하는 벡터를 의미

$e_1 = (cos0^\circ, sin0^\circ) = (1, 0)$

$e_2 = (cos90^\circ, sin90^\circ) = (0, 1)$

 

 

 

2. 각의 측정

• 각도법(Degree)
• 호도법(Radian)

각도법(Degree)

원을 360개로 균일하게 나누고 $^\circ$를 사용해 각을 표현.

왜 360인가? 약수가 많이 나오는 수이기 때문에 원을 쪼개서 계산할 때 유용함.

 

호도법(Redian)

단위 길이 1이라고 하는 것을 기점으로 원을 측정하는 방법.

$1^\circ$를 단위로 삼아 원에 관련된 수학을 전개했을 때 불편한 점이 많기 때문에

별도의 단위를 정하고 이를 기준으로 원에 대한 수학을 전개하는 것이 일반적.

 

호도법의 원리

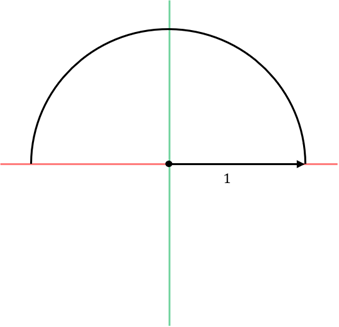
호도법의 전개는 항상 반지름이 1인 단위원을 절반으로 자른 반원을 같이 생각한다.

 

1. 반지름이 1인 반원의 왼쪽 좌표를 원점으로 옮긴다.

 

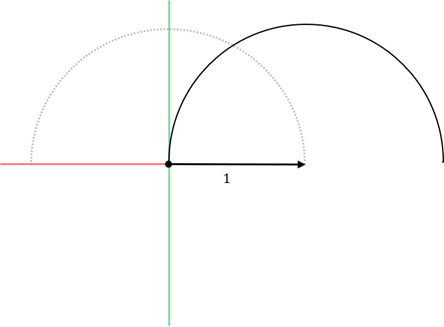
2. 원호를 오른쪽으로 펼친다. → 무리수$\pi$가 나온다. 3.141592...

 

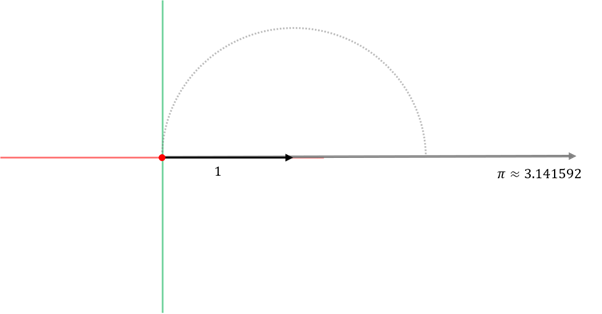
3. 펼쳤던 반원을 원호의 길이가 1이 될 만큼만 되감는다. → 모든 변의 길이가 1인 부채꼴 이 때 나오는 각 역시 무리수이며, 이것이 호도법의 단위인 라디안($rad$). 57.2958...

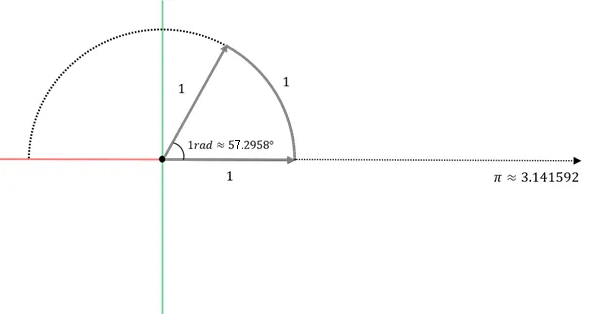
1만큼이 아닌 $\pi$만큼 되감으면 180$^\circ$에 해당하는 반원이 채워짐.

 

이로부터 유도되는 호도법과 각도법의 관계는 다음과 같다.

180$^\circ = \pi(rad)$
1$^\circ = \frec{\pi}{180}(rad)$
1(rad) = $\frec{\pi}{180^\circ}$

 

자주 사용되는 각도에 대응하는 호도값

90$^\circ = \frec{\pi}{2}(rad)$
60$^\circ = \frec{\pi}{3}(rad)$
45$^\circ = \frec{\pi}{4}(rad)$
120$^\circ = \frec{2\pi}{3}(rad)$

 

 

실제 수학에서 사용하는 것과 컴퓨터에서 삼각함수를 다룰 때는 호도법을 기준으로 전개하기 때문에 잘 익혀두어야함.

삼각함수는 주로 '어떤 물체'를 회전시킬 때 사용하게 됨.

 

3. 벡터의 회전(Rotation of Vector)

표준 기저벡터를 사용한 실 벡터공간$\methbb{R}^2$의 원소($x,y$)의 생성 방법

$(x,y) = x(1,0)+y(0,1)$

 

표준 기저벡터를 사용한 실벡터공간 $\methbb{R}^2$의 두 기저 벡터가 새로운 값으로 변한다면,

벡터 공간의 원소($x, y$)는 새로운 두 기저 벡터에 각각 $x$와 $y$를 곱한 벡터에 대응됨.

이 때 새로운 두 기저 벡터의 크기가 1, 직교하는 상태와 현재 방향을 유지하면서 변형하는 것을 회전 변환이라고 한다.

 

각 $\theta$만큼 발생한 회전 변환을 통해 임의의 벡터가 변화되는 과정

 

4. 삼각함수의 역함수(Inverse trigonometric functions)

 

5. 극 좌표계(Polar Coordinate)

 

 

 

---

https://www.inflearn.com/course/%EA%B2%8C%EC%9E%84-%EC%88%98%ED%95%99-%EA%B2%8C%EC%9E%84%EC%97%94%EC%A7%84/dashboard

게임 엔진을 지탱하는 게임 수학 강의 | 이득우 - 인프런