1. 벡터(Vector)의 정의
수 직선에서의 표현의 한계
수를 점으로 표현한다면 1차원의 도형 수직선 위에 있는 것들만 표현이 가능.
1차원 상에서 의미있는 무언가를 표현하기에는 주어진 공간이 너무 부족함.
데카르트 좌표계(Cartesian Coordinate System)
수의 시스템을 기반으로 영역을 확장해 표현하는 방식.
두 실수 집합을 교차시켜서(직교) 평면을 표현하고 오른쪽과 위쪽을 +방향으로 지정한다.

이렇게 영역을 확장한 모습은 두 실수 집합을 곱집합으로 확장한 R⨉R (곱집합으로 구성된 평면)로 볼 수 있다.
곱집합의 원소는 순서쌍이므로 두 집합의 원소를 각각 미지수 x와 y로 두면 이는 (x, y)로 표현할 수 있다.
이를 좌표(Coordinate)라고 함.
직교한다: 90도로 배치한다는 의미를 넘어 가로축에 있는 실수 집합과 세로축에 있는 실수 집합이
서로 연관성이 없다는 것을 의미
2차원 평면의 시각화
좌표에 해당하는 대상을 점으로 표현하면 다음과 같다.
수와 동일하게, 지정한 위치에 점을 찍거나 원점으로부터 화살표로 가리키는 두 가지 표현 방식이 있음.
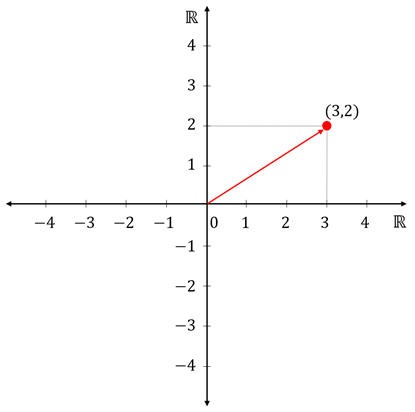
언제 점을 찍을지, 언제 화살표로 표현(방향)할지는 '아핀 공간(Affine Space)'에서 사용됨
직선과 평면의 비교

이러한 확장된 실수의 곱집합 R⨉R 의 공간 체계가 '수'는 아니기 때문에 이 대상을 규정할 필요가 있다.
벡터(Vector)와 벡터 공간(Vector Space)
이 대상은 특정 수 집합을 지정하는 것이 아닌, 보편적인 수의 구조를 사용해 정의함.
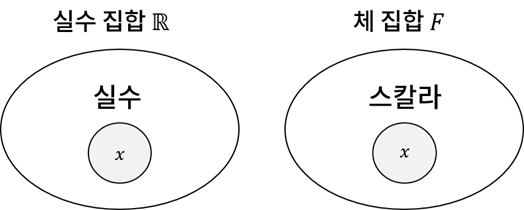

벡터 공간은 집합, 벡터는 그 집합의 원소의 개념.
- 집합: 체의 성질을 가지는 수 집합의 곱집합으로부터 만들어낸 대상
- 원소: 스칼라의 순서쌍
실제로는 수 집합, 실수를 사용하지만 체 집합의 관점에서 곱집합을 이룬다는, 좀 더 넓은 관점에서 이해하면 좋음
→ 두 개의 채집합의 곱집합. 체 집합의 원소는 스칼라, 스칼라들을 순서쌍으로 조합한 요소가 벡터.
구조적인 관점에서 벡터 공간과 벡터를 정의할 수 있게 됨.
2. 벡터의 연산(Vector Operations)
벡터 공간이 변환되기 위해서는 수의 이항 연산과 같이 벡터를 사용해 새로운 벡터를 생성하는 시스템이 필요.
이를 위한 벡터 공간의 기본 연산이 정의되어 있음.
벡터의 기본 연산
벡터와 벡터의 덧셈
- (a, b) + (c, d) = (a + c, b + d)

물 10ml와 기름 20ml가 담긴 컵이 있다. 여기에 물 30ml와 기름 10ml가 담긴 컵을 서로 혼합할 때
만들어지는 물과 기름의 양은? 40ml, 30ml
두 실수 집합이 직교한다는 것은 물과 기름처럼 서로 연관성 없이 독립적으로 동작함을 의미.
벡터와 벡터의 덧셈은 x만큼 평행이동, y만큼 평행이동하는 결과를 가져옴.
벡터와 스칼라의 곱셈
어떤 수 집합을 쓰냐에 따라 스칼라가 달라질 수 있음 (실수, 유리수 등)
- $k ∙ (a, b) = (ka, kb)$
- $ (a, b) ∙ k = (ak, bk) $
k도 스칼라, a, b도 스칼라이기 때문에 교환법칙이 성립, $ka$와 $ak$는 같다.

원점을 중심으로 어떤 벡터를 생성했을 때 벡터가 가지고 있는 기울기를 따라서 형성된 무한대의 직선이 있고,
벡터와 스칼라의 곱셈으로 생성된 새로운 벡터는 언제나 무한대 직선 위에 위치함.
어찌보면 1차원적인 벡터의 생성 방법이라고도 할 수 있음.
벡터와 스칼라의 곱셈은 벡터와 같은 기울기를 가지는 1차원 벡터를 생성함.
이후 실제 응용을 위한 연산
- 벡터의 내적(Dot Product)
- 벡터의 외적(Cross Product)
벡터의 크기(Norm)
수의 크기 = 원점으로부터의 거리 $ |x| $
벡터의 크기 = 원점으로부터의 최단 거리 $ |v|= \sqrt{x^2+y^2} $. 노름(Norm)이라고도 함.
벡터의 크기는 $||v||$로도 표현하지만 여기서는 간결하게 $|v|$로 표기.

어떤 평면에서 원점으로부터의 최단거리는 그림과 같이 직각삼각형의 빗변 길이를 의미.
피타고라스 정리($a^2+b^2=c^2$)로 빗변의 길이를 구할 수 있음
단위 벡터: 크기가 1인 벡터
벡터의 크기과 역수(Reciprocal)를 곱하면 단위 벡터가 만들어짐.
단위 벡터를 만드는 공식: $\hat{u}=\frac{v}{|v|}$
3. 벡터 공간의 공리
이런한 벡터의 연산은 벡터 공간이라는 큰 집합의 개념에서 새로운 벡터를 생성하는 닫힌 시스템으로 바라봐야함.
이러한 벡터 공간의 시스템은 항상 수를 시스템적인 측면에서 분석한
체(Field)의 시스템을 기반으로 확장해 만든 것으로 볼 수 있으며, 이는 8개의 공리로 구성되어 있다.
이 '체'라는 연산에 대한 공리를 만족하면 어떤 시스템이 된다 라고 규정하는 것.
→ 구조적으로 벡터 공간이라고 하는 시스템을 바라볼 수 있는 기반
참고: $u, v, w$는 벡터를 의미하고, $a, b$는 스칼라를 의미함
- 덧셈 연산의 결합법칙 (벡터와 벡터)
$u + (v+w) = (u+v)+w$
$u, v, w$는 체 집합의 요소인 스칼라이고, 체 집합은 결합 법칙이 성립함. - 덧셈 연산의 교환법칙
$u+v = v+u$
체집합에 기반을 둔 벡터 시스템 상 당연히 법칙이 성립. - 덧셈 연산의 항등원
$v+\vec{0}=v, \vec{0}$ ($\vec{0}$은 모든 요소가 0인 영벡터를 의미)
영벡터가 있을 때 각각에 대해서 0을 더하면 항등원이 0이기 때문에 결국 그 벡터의 값은 변하지 않음
→ 벡터 공간에서 덧셈 연산의 항등원은 0벡터 - 덧셈 연산의 역원
$v+(-v) = \vec{0},$ $-v$
영벡터를 만들기 위해서는 그 벡터에 마이너스를 붙여준, 반대 방향으로 향하는 벡터를 더해줌. - 스칼라 곱셈 연산의 호환성(Compatiblilty)
$a(bv) = (ab)v$
스칼라 곱셈에서는 스칼라 값을 어떤 걸 쓰든, 순서가 어떻든 결과는 동일하다.
벡터 공간이라는 것이 벡터들로만 이루어진 것이 아닌, 체 라고 하는 수 집합의 구조가 기반됨.
그렇게 때문에 벡터 공간은 overfield, 체집합의 기반 위에서 항상 '스칼라'라는 요소를 같이 고려해야 함.
→ 수 집합과 벡터의 차이. - 스칼라 곱셈 연산의 항등원
$1v = v, 1$
각 요소에 스칼라 1을 곱해주면 동일한 결과가 나옴. - 벡터 덧셈과 스칼라 곱셈의 분배법칙
$a(u+v) = au+av$
덧셈 연산을 적용하는 원소가 벡터인 경우, $a(u+v)$의 형태가 나오게 되고,
이는 각각에 스칼라 값을 곱한 결과와 동일함 - 스칼라 덧셈과 스칼라 곱셈의 분배법칙
$(a+b)v = ab + bv$
덧셈 연산을 적용하는 원소가 스칼라일 경우 $(a+b)v$의 형태,
벡터와 마찬가지로 각각을 개별적으로 곱한 것과 동일함
만일 벡터 공간의 기반을 이루는 체 집합으로 실수 집합 $\mathbb{R}$을 사용하는 경우,
이를 실 벡터 공간(real vector space)이라고 함.
이러한 실 벡터 공간으로 컴퓨터 그래픽스를 구현.
게임 엔진을 지탱하는 게임 수학 강의 | 이득우 - 인프런
이득우 | , 3D 게임 프로그래밍, 본질을 알아야 더 잘 할 수 있어요! 🎮 게임 프로그래밍, 한 단계 나아서고 싶다면? 안녕하십니까? 청강문화산업대학교 게임콘텐츠스쿨에서 학생들에게 게임 프
www.inflearn.com
'게임 개발 > 게임 수학' 카테고리의 다른 글
| 게임 수학 - 삼각 함수 (1) | 2025.02.26 |
|---|---|
| 게임 수학 - 선형 독립 (0) | 2025.02.25 |
| 게임 수학 - 함수 (0) | 2025.02.04 |
| 게임 수학 - 수의 구조 (0) | 2025.01.22 |
| 기초 수학 - 로그 (0) | 2024.07.23 |